hiltpubli.blogg.se - Moment of inertia equation for rectangle

MOMENT OF INERTIA EQUATION FOR RECTANGLE FREE

Support Reactions - Equilibrium Static equilibrium is achieved when the resultant force and resultant moment equals to zero.

Structural Lumber - Section Sizes Basic size, area, moments of inertia and section modulus for timber - metric units.

Rotating Shafts - Torque Torsional moments acting on rotating shafts.

Radius of Gyration in Structural Engineering Radius of gyration describes the distribution of cross sectional area in columns around their centroidal axis.

Pipe Formulas Pipe and Tube Equations - moment of inertia, section modulus, traverse metal area, external pipe surface and traverse internal area - imperial units.

Flywheels - Kinetic Energy The kinetic energy stored in flywheels - the moment of inertia.

Euler's Column Formula Calculate buckling of columns.

Conn-Rod Mechanism The connecting rod mechanism.

Center Mass Calculate position of center mass.

Cantilever Beams - Moments and Deflections Maximum reaction forces, deflections and moments - single and uniform loads.

Area Moment of Inertia Converter Convert between Area Moment of Inertia units.

Area Moment of Inertia - Typical Cross Sections II Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles.

Area Moment of Inertia - Typical Cross Sections I Typical cross sections and their Area Moment of Inertia.

American Wide Flange Beams American Wide Flange Beams ASTM A6 in metric units.

Statics Loads - forces and torque, beams and columns.

Mechanics Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more.

Dynamics Motion - velocity and acceleration, forces and torque.

Basics The SI-system, unit converters, physical constants, drawing scales and more.

Moments of Inertia for a slender rod with axis through end can be expressed as Moments of Inertia for a slender rod with axis through center can be expressed as Moments of Inertia for a rectangular plane with axis along edge can be expressed as Moments of Inertia for a rectangular plane with axis through center can be expressed as R = radius in sphere (m, ft) Rectangular Plane

R = distance between axis and hollow (m, ft) Solid sphere R = distance between axis and outside disk (m, ft) Sphere Thin-walled hollow sphere R = distance between axis and outside cylinder (m, ft) Circular Disk R o = distance between axis and outside hollow (m, ft) Solid cylinder R i = distance between axis and inside hollow (m, ft) R o = distance between axis and outside hollow (m, ft) Hollow cylinder R = distance between axis and the thin walled hollow (m, ft) Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass (1) and can be expressed as: Some Typical Bodies and their Moments of Inertia Cylinder Thin-walled hollow cylinder Radius of Gyration in Structural Engineering I = moment of inertia for the body ( kg m 2, slug ft 2) The Radius of Gyration for a body can be expressed as The Radius of Gyration is the distance from the rotation axis where a concentrated point mass equals the Moment of Inertia of the actual body.

K = inertial constant - depending on the shape of the body Radius of Gyration (in Mechanics) + m n r n 2 (2)įor rigid bodies with continuous distribution of adjacent particles the formula is better expressed as an integralĭm = mass of an infinitesimally small part of the body Convert between Units for the Moment of InertiaĪ generic expression of the inertia equation is I = ∑ i m i r i 2 = m 1 r 1 2 + m 2 r 2 2 +. Point mass is the basis for all other moments of inertia since any object can be "built up" from a collection of point masses. = 1 kg m 2 Moment of Inertia - Distributed Masses The Moment of Inertia with respect to rotation around the z-axis of a single mass of 1 kg distributed as a thin ring as indicated in the figure above, can be calculated as

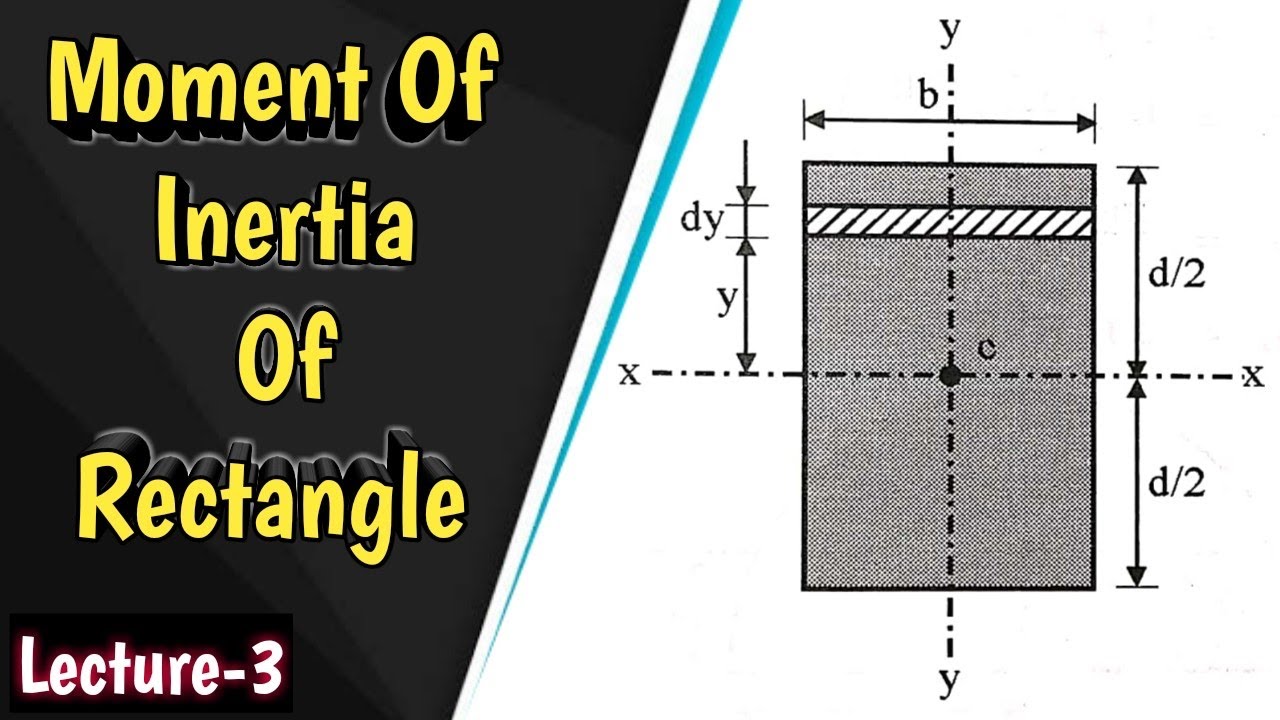
MOMENT OF INERTIA EQUATION FOR RECTANGLE FREE

Make 3D models with the free Engineering ToolBox Sketchup Extension R = distance between axis and rotation mass (m, ft) Example - Moment of Inertia of a Single Mass I = moment of inertia ( kg m 2, slug ft 2, lb f fts 2) Moment of Inertia of a body depends on the distribution of mass in the body with respect to the axis of rotationįor a point mass the Moment of Inertia is the mass times the square of perpendicular distance to the rotation reference axis and can be expressed as.Moment of Inertia has the same relationship to angular acceleration as mass has to linear acceleration. Mass Moment of Inertia (Moment of Inertia) - I - is a measure of an object's resistance to change in rotation direction.